Surface metrology

Surface metrology is the measurement of small-scale features on surfaces, and is a branch of metrology. Surface primary form, surface waviness and surface roughness are the parameters most commonly associated with the field. It is important to many disciplines and is mostly known for the machining of precision parts and assemblies which contain mating surfaces or which must operate with high internal pressures.

Surface metrology is the study of surface geometry, also called surface texture or surface roughness. The approach is to measure and analyze the surface texture in order to be able to understand how the texture is influenced by its history, (e.g., manufacture, wear, fracture) and how it influences its behavior (e.g., adhesion, gloss, friction).

Contents

Equipment

A full list of standardized instruments can also be found in the part 6 document of the ISO series ISO 25178.

Contact (tactile measurement)

The following instruments are well established technologies. There are many manufacturers implementing these technologies into products:

Non-Contact (optical microscopes)

Optical measurement instruments have some advantages over the tactile ones. The main advantages are:

Vertical scanning:

Horizonal scanning:

Choice of the right measurement instrument

Because of every instrument has advantages and disadvantages the operator must choose the right instrument depending on the measurement application. In the following some advantages and disadvantages to the main technologies are listed:

Resolution

The scale of the desired measurement will help decide which type of microscope will be used.

For 3D measurements, the probe is commanded to scan over a 2D area on the surface. The spacing between data points may not be the same in both directions.

In some cases, the physics of the measuring instrument may have a large effect on the data. This is especially true when measuring very smooth surfaces. For contact measurements, most obvious problem is that the stylus may scratch the measured surface. Another problem is that the stylus may be too blunt to reach the bottom of deep valleys and it may round the tips of sharp peaks. In this case the probe is a physical filter that limits the accuracy of the instrument.

Roughness parameters

Main article: Roughness#Parameterization

The real surface geometry is so complicated that a finite number of parameters cannot provide a full description. If the number of parameters used is increased, a more accurate description can be obtained. This is one of the reasons for introducing new parameters for surface evaluation. Surface roughness parameters are normally categorised into three groups according to its functionality. These groups are defined as amplitude parameters, spacing parameters, and hybrid parameters.[3]

Profile roughness parameters

Parameters used to describe surfaces are largely statistical indicators obtained from many samples of the surface height. Some examples include:

Table of useful surface metrics
Parameter Name Description Type Formula
Ra, Raa, Ryni arithmetic average of absolute values Mean of the absolute values of the profile heights measured from a mean line averaged over the profile Amplitude 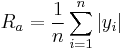R_a = \frac{1}{n} \sum_{i=1}^{n} \left | y_i \right |
Rq, RRMS root mean squared Amplitude 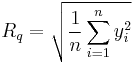R_q = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} y_i^2 }
Rv maximum valley depth Maximum depth of the profile below the mean line with the sampling length Amplitude 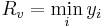R_v = \min_{i} y_i
Rp maximum peak height Maximum height of the profile above the mean line within the sampling length Amplitude 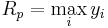R_p = \max_{i} y_i
Rt Maximum Height of the Profile Maximum peak to valley height of the profile in the assessment length Amplitude 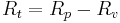R_t = R_p - R_v
Rsk Skewness Symmetry of the profile about the mean line Amplitude 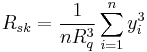R_{sk} = \frac{1}{n R_q^3} \sum_{i=1}^{n} y_i^3
Rku Kurtosis Measure of the sharpness of the surface profile Hybrid 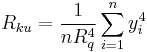R_{ku} = \frac{1}{n R_q^4} \sum_{i=1}^{n} y_i^4
RSm Mean Peak Spacing Mean Spacing between peaks at the mean line Spatial 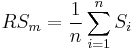RS_{m} = \frac{1}{n} \sum_{i=1}^{n} S_i

This is a small subset of available parameters described in standards like ASME B46.1[4] and ISO 4287[5]. Most of these parameters originated from the capabilities of profilometers and other mechanical probe systems. In addition, new measures of surface dimensions have been developed which are more directly related to the measurements made possible by high-definition optical gauging technologies.

Most of these parameters can be estimated using the SurfCharJ plugin [1] for the ImageJ.

Areal surface parameters

The surface roughness can also be calculated over an area. This gives Sa instead of Ra values. The ISO 25178 series describes all these roughness values in detail. The advantage over the profile parameters are:

Surfaces have fractal properties, multi-scale measurements can also be made such as Length-scale Fractal Analysis or Area-scale Fractal Analysis.[6]

Filtering

To obtain the surface characteristic almost all measurements are subject to filtering.

References

  1. ^ F. Gao, R.K. Leach, J. Petzing and J.M. Coupland: Surface Measurement errors using commercial scanning white light interferometers. In Measurement Science and Technology, 19 (1), 015303 , Jan. 2008
  2. ^ Hyug-Gyo Rhee, Theodore Vorburger, Jonathan W. Lee and Joseph Fu: Discrepancies between roughness measurements obtained with phase-shifting and white-light interferometry. Applied Optics IP, vol. 44, Issue 28, pp.5919-5927, 2005
  3. ^ Gadelmawla E.S.; Koura M.M.; Maksoud T.M.A.1; Elewa I.M.; Soliman H.H., Roughness parameters, Journal of Materials Processing Technology, Volume 123, Number 1, 10 April 2002 , pp. 133-145(13)
  4. ^ ASME B46.1
  5. ^ ISO 4287
  6. ^ http://www.me.wpi.edu/Research/SurfMet/Research/fractal.html